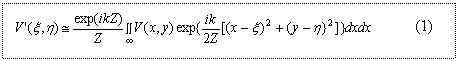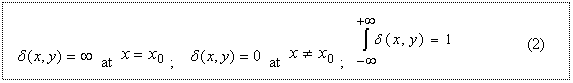1. ДВА ВИДА ЭЛЕМЕНТАРНЫХ СВЕТОВЫХ РАСПРЕДЕЛЕНИЙ

    1.1 Световое распределение, порождаемое 3Д сценой в свободном пространстве

    Произвольный объект наблюдаемой 3Д сцены можно представить совокупностью S точечных источников света (рис.1), которые порождают световое распределение V (x,y) (далее обозначаемое как V), распространяющееся в качестве оптической волны через слой (объем) свободного пространства протяженностью Z и достигающее глаз наблюдателя в форме светового распределения V’ (ξ,η) (далее - V’), которое связано с распределением V известной интегральной формулой Френеля-Кирхгофа (1).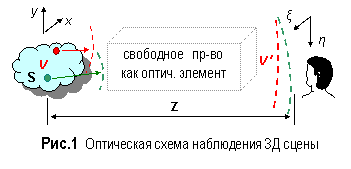


    Зрение человека воспринимает световое распределение V’, по результатам этого восприятия в сознании человека формируется виртуальный образ 3Д сцены, т.е. восстановленное в виртуальном виде распределение V.
    Для элементарного 3Д объекта наблюдаемой сцены, представленного в виде одиночного точечного источника 0 света с координатами (x₀, y₀), соответствующее световое распределение V выражается дельта-функцией δ(х₀,y₀) (2)
подстановка которой в (1) дает поступающее в глаза наблюдателя 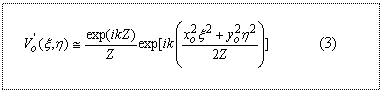световое распределение V’₀ (3) от точечного источника 0 света в форме сферической волны, радиус кривизны которой несет информацию о расстоянии Z от наблюдателя до данного источника, интенсивность которой пропорциональна интенсивности источника и обратно пропорциональна расстоянию Z, а угол наклона фронта сферической волны (относительно уровня расположения глаз наблюдателя) определяется координатами (x0, y0) источника.

    Для случая свободного пространства справедлив принцип суперпозиции, т.е. отклик оптической системы в целом на сложный пространственный оптический сигнал равен сумме откликов на элементарные оптические сигналы. Поэтому произвольная 3Д сцена, представленная суперпозицией точечных источников света, воспринимается зрением в форме суммы всех сферических волн, порождаемых указанными источниками. Эта сумма представлена, как видно из предыдущего рассмотрения, множеством сферических волн с разным углами наклона директора волнового фронта, что кратко определяется как угловой спектр сферических волн. Физическое описание описанного распространения света в свободном пространстве есть френелевская дифракция (дифракция Френеля) для случая конечной величины Z (в пределе при Z → ∞ имеет место дифракция Фраунгофера, которая при выбранном способе рассмотрения является частным случаем дифракции Френеля, и поэтому достаточно рассматривать только последнюю при рассмотрении 3Д дисплеев во всех ситуациях на практике).

    Объектное представление 3Д сцены есть представление «по точкам» объектов этой сцены в световом распределении, порождаемым рабочей средой М (рис.2). В этом случае зрение воспринимает совокупность сферических волн V’.
    Дифракционное представление 3Д сцены (френелевской дифракцией или угловым спектром сферических волн) есть представление этой сцены в рабочей среде М сферическими волнами (назовем их «первичными»), которые после прохождения слоя Z пространства воспринимаются зрением в форме «вторичных» волн (рис. 3). 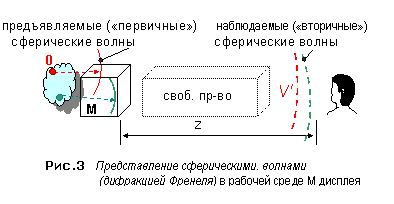Как «первичные», так и «вторичные» сферические волны описываются формулой (1), представляющей пространственный угловой спектр сферических волн, представляющих 3Д сцену посредством френелевской дифракции.
    Рассмотрим требуемую размерность светового распределения, формируемого в рабочей среде М дисплея, т.е. число пространственных координат, необходимых для описания этого распределения. Способность трехкоординатного (3Д) светового распределения самостоятельно представлять 3Д сцену очевидна (3Д сцена в природе всегда представлена трехкоординатным световым распределением). Способность двухкоординатного (2Д) светового распределения самостоятельно представлять 3Д сцену вытекает из свойств бинокулярного зрения человека.
    Рассмотрим, есть ли смысл выделять однокоординатное (1Д) световое распределение как самостоятельное в проводимой классификации. Очевидно, что однокоординатное (одномерное) световое распределение само по себе не способно представить полноценную информацию обо всех трех координатах 3Д сцены, но однокоординатное световое распределение возможно использовать в 3Д дисплее как промежуточный результат за счет использования свойства кратковременной памяти зрения человека, которое способно объединять в единую 2Д картину ряд предъявляемых (последовательно во времени) 1Д световых распределений, если частота предъявления не ниже некоторой критической частоты. Поэтому всегда использование 1Д световых распределений сводится к формированию эквивалентных 2Д световых распределений на сетчатках глаза или на промежуточных экранах или в рабочей среде (характеризующихся свойством кратковременной или долговременной памяти), следовательно, 1Д световое распределение не имеет смысла выделять как самостоятельный параметр классификации.